本章のあらすじ

• ぐるぐる回す
• 滑らかな波を描く
• マウスカーソルを目玉で追いかける

円周上の波にさらに波を重ねて点を打つ

三角関数

三角関数とは？

高校時代に習った（はず）のアレ。サイン、コサイン、タンジェント、…。苦手だった人も少なくないでしょう。

学問的な側面を理解しておくことは（最終的には）大切ですが、今回は触れません。その便利な性質だけをつまみ食いして、これまでできなかった表現を作るところからはじめてみましょう。

角度から座標を計算する

三角関数のサイン sin() とコサイン cos() を利用すると、角度からXYの位置を計算できます。

See the Pen sin, cos by cocopon (@cocopon) on CodePen.

例えば角度が angle のとき、 cos(angle) がX方向の距離、 sin(angle) がY方向の距離です。円の大きさは 1 でとても小さいので、大きな数値を掛け算して使うことが多いです。

角度の単位が「ラジアン」となっていることに気をつけましょう。1周つまり360(度)は、2π(ラジアン) = 2 * 3.14… = 6.28… に相当します。

回す

キャンバスの中央から線を引き、先端に円を描きます。このときの角度を少しずつ増やしていくと、回転させることができます。 （→rotation）

// 角度
float angle;

void setup() {
  size(600, 600);
  fill(0);

  angle = 0;
}

void draw() {
  background(255);

  // 角度を少しずつ増やす
  angle += 0.05;

  // キャンバスの中心座標
  float cx = width / 2;
  float cy = height / 2;

  // cos(), sin() で角度に対するX座標とY座標を計算
  // 線を描く
  line(
    cx, cy,
    cx + cos(angle) * 150,
    cy + sin(angle) * 150
  );
  // 円を描く
  ellipse(
    cx + cos(angle) * 150,
    cy + sin(angle) * 150,
    20, 20
  );
}

往復運動

このまま cos() の結果に 0 を掛け算して、左右の動きを封じてみましょう。どんな動きになるでしょうか？

ellipse(
  cx + cos(angle) * 0,
  cy + sin(angle) * 150,
  20, 20
);

同じ場所を往復する動きになりました。緩急もいい感じについているので、便利な使いどころがたくさんありそうです。

うずまき

左右の固定を元に戻して、角度に応じて中心から離れるようにしてみましょう。

// 角度の増加に応じて、中心からの長さも増やす
float len = angle * 10;

// cos(), sin() で角度に対するX座標とY座標を計算
// 円を描く
ellipse(
  cx + cos(angle) * len,
  cy + sin(angle) * len,
  10, 10
);

背景をクリアせず描きっぱなしにすれば…うずまきの完成です。 （→spiral）

リサジュー曲線

先の例の cos(), sin() 関数に指定している angle について、適当な整数の値を掛け算してみましょう。

int a = 7;
int b = 3;
ellipse(
  cx + cos(angle * a) * 150,
  cy + sin(angle * b) * 150,
  2, 2
);

円のサイズも小さくしました。どんな模様ができるでしょうか？ （→lissajous）

なかなかおもしろい模様が出てきました。この曲線は、考案者の名前にちなんで「リサジュー曲線」と呼ばれます。

発展

• パラメーターを変えると模様はどのように変化するだろうか？
• 描画を高速化できないだろうか？（ draw() ブロック内の処理を何度も繰り返し実行するには…？）
• 点ではなく線でつなげられるだろうか？

波打つ

往復運動のもとになっている sin() 関数は、グラフでみるとこのような波の形（正弦波）になります。

y = sin(x) のグラフ

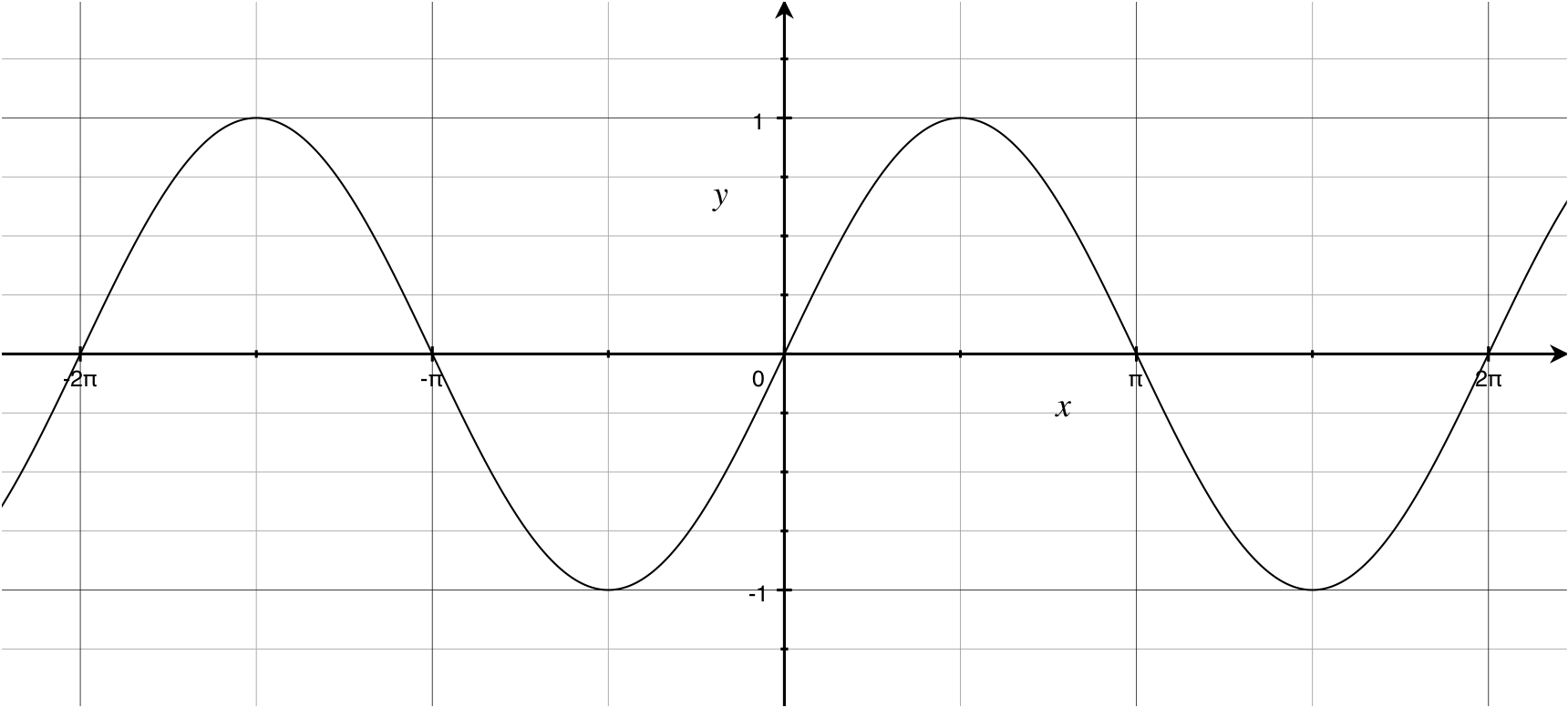
Processingでもこの波を描いてみましょう。for文でX座標を 0 から width まで変化させながら、各X座標における sin() を計算して点を描いていきます。 （→wave）

void setup() {
  size(600, 600);
  noStroke();

  background(255);
  fill(0);
  for (int x = 0; x < width; x += 1) {
    // x をそのまま使うと変化が大きすぎるので、小さな数値を掛けておく
    float y = height / 2 + sin(x * 0.01) * 100;
    rect(x, y, 1, 1);
  }
}

sin() の中の x や外側に掛かっている数値をいろいろ変えながら、波がどのように変化するか実験してみてください。

もっと波に触れてみる

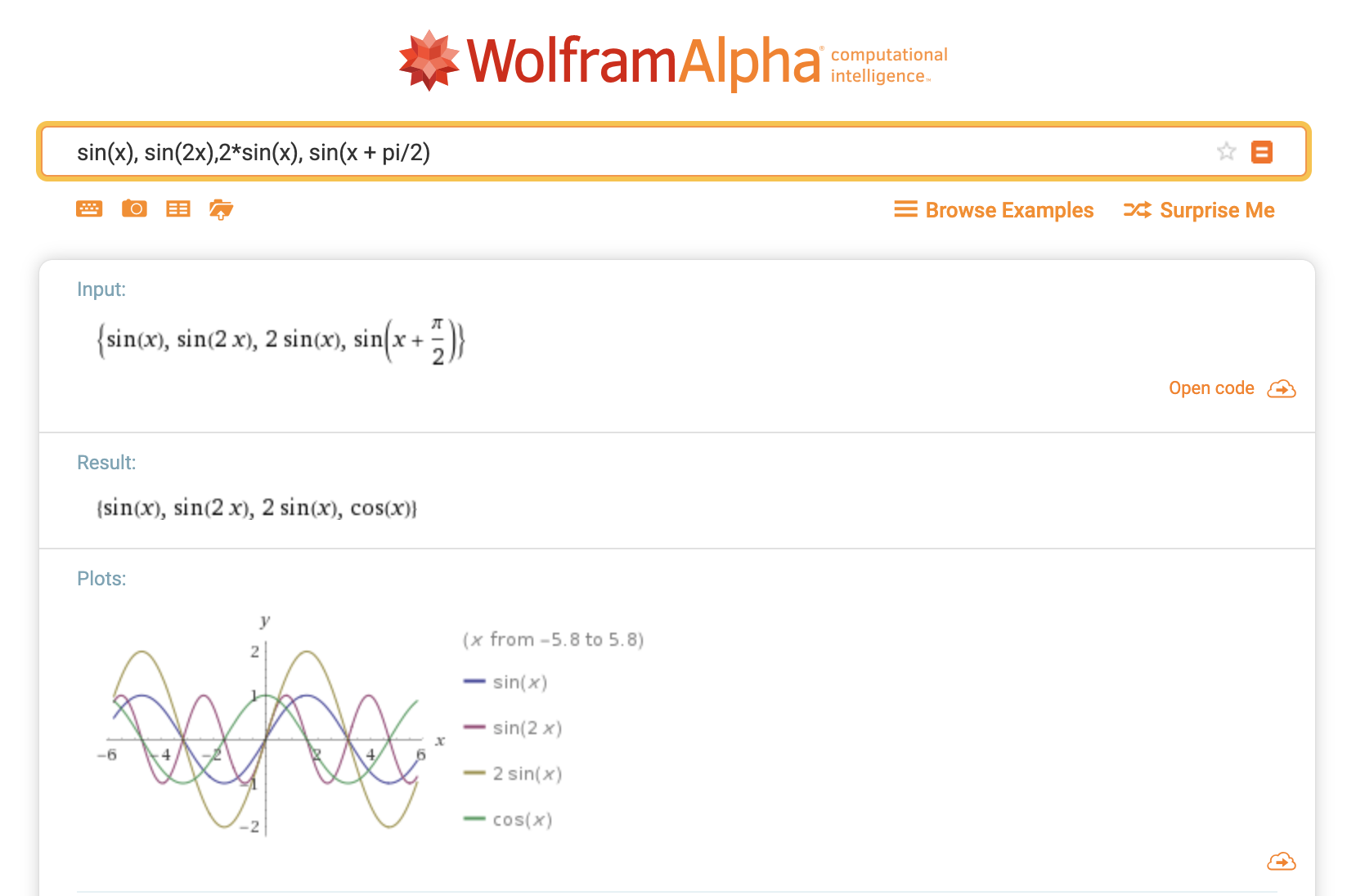
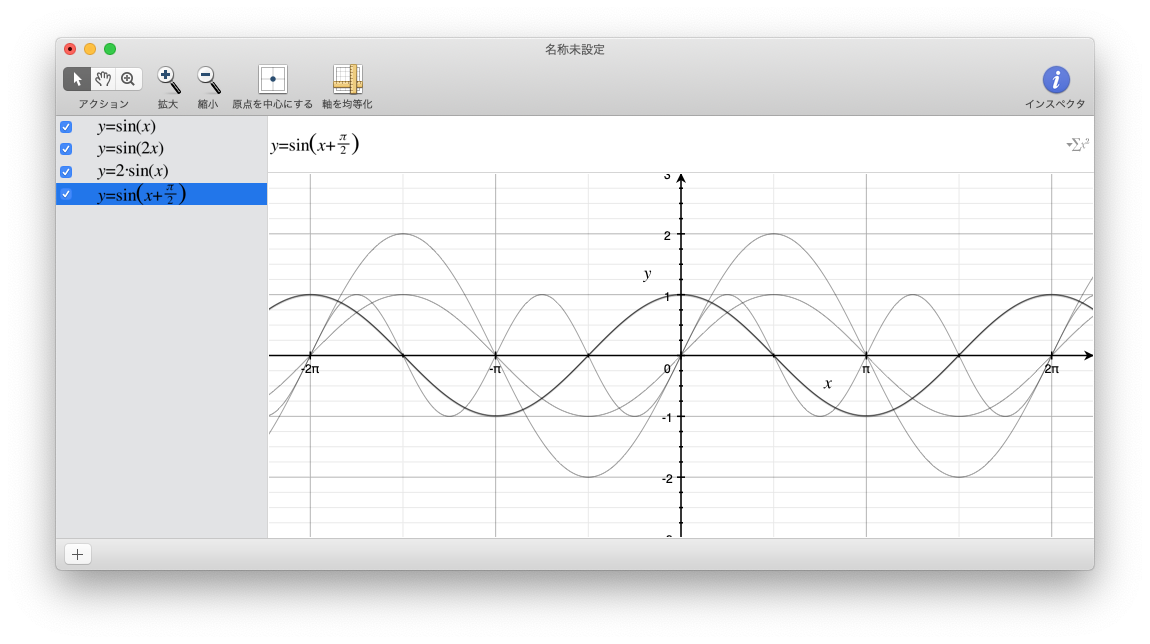
正弦波に興味を持った人は、Wolfram Alphaなどのサービスを使うとさらに手軽に実験できます。

例えば sin(x), sin(2x), 2*sin(x), sin(x + pi/2) のように入力することで、それぞれの式がどのような波形になるかを簡単に確認できます。

Wolfram Alphaによる波形の確認

macOSをお使いの人は、標準付属の「Grapher」というアプリを使うのもおすすめです。

Grapherによる波形の確認

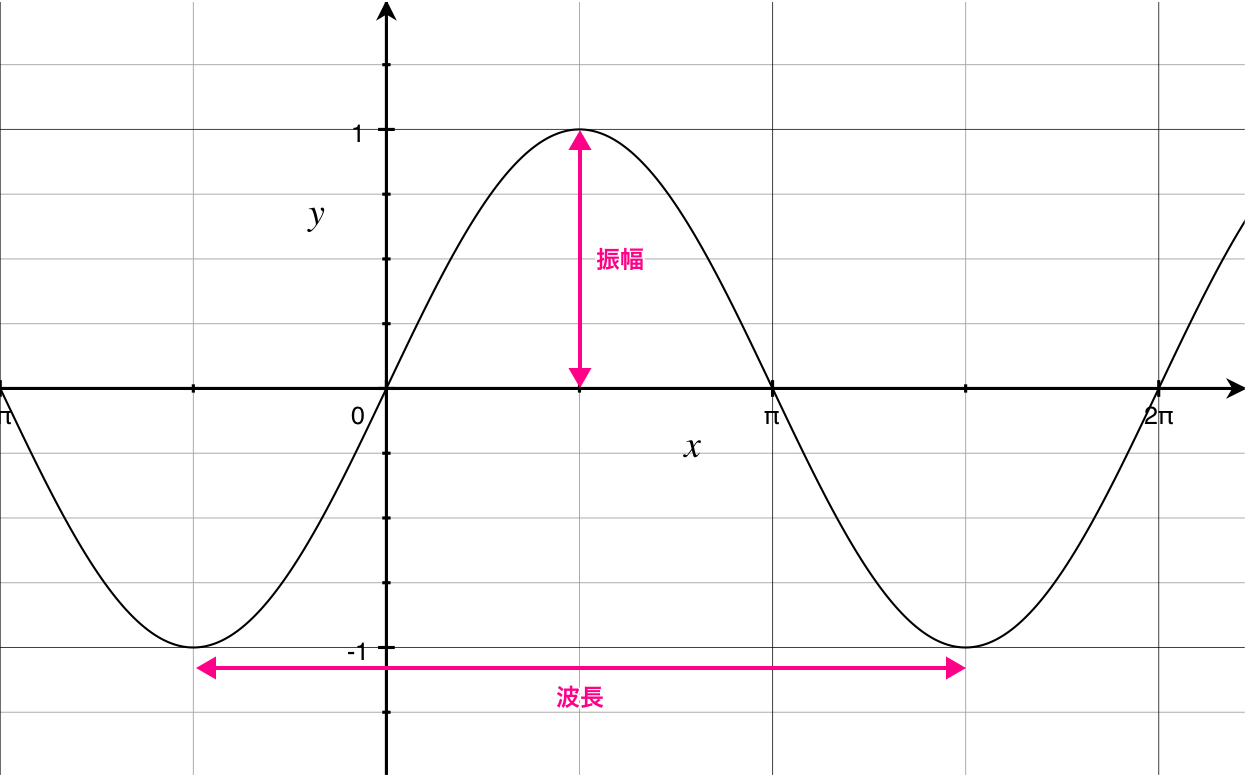
ちなみに、波の大きさ・振れ幅を「振幅」、山同士の間隔を「波長」と呼びます。余裕があれば覚えておくとよいでしょう。

振幅と波長

練習：波を重ねてみる

さて、先ほどのスケッチに戻りましょう。カーソル位置に応じて振幅や波長を変化させつつ、さまざまな波を重ね描きするとどうなるでしょうか？

まず、Y座標の計算時にカーソル位置を反映するよう書き換えます。

    float y = height / 2 + sin((x + mouseX) * 0.01) * mouseY;

次に、マウスをドラッグするたびに波を描くよう、描画処理を mouseDragged() ブロックに移動しましょう。重ね描きするので塗り色は薄めに。

void mouseDragged() {
  fill(0, 20);

  for (int x = 0; x < width; x += 1) {
    float y = height / 2 + sin((x + mouseX) * 0.01) * mouseY;
    rect(x, y, 1, 1);
  }
}

さて、どのような絵が描けましたか？ （→wave_mouse）

発展

• 振幅や波長に応じて塗り色を変えると？
• 小さな rect() ではなく、他のサイズや図形で描くと？

追いかける

atan2() 関数を使うと、 atan2( Y方向の距離 , X方向の距離 ) で角度を計算できます。 sin() と cos() は角度から座標を計算する機能を持っていたので、ちょうどその逆ですね。

下のスケッチはキャンバス中心からカーソルまでの距離を計算・可視化しています。触りながら感覚を掴んでみてください。

See the Pen Trigonometric functions (atan2) by cocopon (@cocopon) on CodePen.

これを応用すると、例えば目玉の中心からカーソルまでの角度を計算して、黒目をそちらに向ける…なんてことも可能になります。 （→eyes）

// 白目
fill(255);
ellipse(ox, oy, 100, 100);

// 目からカーソルまでの角度を計算
float angle = atan2(mouseY - oy, mouseX - ox);

// 指定した角度の位置に黒目を描く
fill(0);
ellipse(
  ox + cos(angle) * 20, oy + sin(angle) * 20,
  50, 50
);

本章のまとめ

• 三角関数（ sin(), cos() ）は、角度から位置を計算する道具として便利に使える
• 三角関数の力を借りると、ものを回したり波を描いたりできる
• 逆に位置から角度を計算することもできる（ atan2() ）