整列(for文)
本章のあらすじ
- 図形を1方向(縦または横)に整列する
- 図形を2方向(縦横)に整列する

繰り返し
「大量生産(while文)」の回では、繰り返し処理によって図形が大量生産できることを学びました。 今回は繰り返しのより効率的な書きかたを学びつつ、大量生産した図形を整列させる方法について見ていきましょう。
復習:while文
以前、クリックした位置に波紋を描くスケッチを作りましたね。答えを見ないでコードを再現できるでしょうか?

void setup() {
size(600, 600);
background(255);
noFill();
stroke(0);
}
void mousePressed() {
// 繰り返し回数を決めるループ変数を宣言・初期化
int i = 0;
// i が 20 より小さいとき、ブロックを繰り返す
// ブロックの最後で 1 ずつ足しているので、計 20 回繰り返すことになる
while (i < 20) {
// ループ変数を円の大きさに反映して描く
ellipse(mouseX, mouseY, i * 10, i * 10);
// i を 1 増やして繰り返す
i = i + 1;
}
}
void draw() {
}繰り返し回数の決まったwhile文を書く際は、
- ループ変数を宣言・初期化する
- 繰り返しを継続する条件(継続条件)を書いてループを回す
- ループ変数を更新する(更新処理)
という決まった流れがあることに気づいたでしょうか。
// 1. ループ変数を宣言・初期化する
int i = 0;
// 2. 繰り返しを継続する条件を書いてループを回す
while (i < 20) {
ellipse(mouseX, mouseY, i * 10, i * 10);
// 3. ループ変数を更新する
i = i + 1;
}この流れは頻繁に使われるので、一気にまとめて書く方法が用意されています。それが「for文」です。
もうひとつの繰り返し: for 文
for文も、while文と同様に処理を繰り返すための文です。
繰り返し回数を決めるために、Processingのfor文では ; で区切られた3つの部分「初期化」「継続条件」「更新処理」が用意されています。
for ( 初期化 ; 継続条件 ; 更新処理 ) {
// 繰り返し実行するブロック
}より具体的なコードを見てみましょう。
for (int i = 0; i < 20; i = i + 1) {
ellipse(mouseX, mouseY, i * 10, i * 10);
}それぞれの部分の意味は以下のとおりです。
| 部分 | コード | 意味 |
|---|---|---|
| 初期化 | int i = 0 | ループ変数 i を宣言、 0 を代入 |
| 継続条件 | i < 20 | i が 20 より小さいなら繰り返す |
| 更新処理 | i = i + 1 | i を 1 増やす |
これは、以下のwhile文と同じ構造ですね。
// 初期化
int i = 0;
while (i < 20) { // 継続条件
ellipse(mouseX, mouseY, i * 10, i * 10);
// 更新処理
i = i + 1;
}どのように繰り返しているのか、1ステップずつ見てみましょう。








繰り返す回数が決まっている場合は、for文のほうが書きやすく多用されます。ループ変数を更新し忘れて無限ループに陥る危険性も抑えられます。慣れると便利なので、積極的に使っていきましょう。
// 読みかたの例
// 変数 i を 0 ~ 19 まで、 1 ずつ増やしながら繰り返す
for (int i = 0; i < 20; i = i + 1) {
// i: 0, 1, 2, …, 19
}
// 変数 i を 0 ~ 600 まで、 100 ずつ増やしながら繰り返す
for (int i = 0; i <= 600; i = i + 100) {
// i: 0, 100, 200, …, 600
}変数の再代入の省略記法
練習用のスケッチを書きはじめる前に、再代入の省略記法を知っておきましょう。
これまで、変数に値を足したり引いたりと、いわゆる「再代入」する場合は以下のようなコードを書いていました。
// i を 2 増やす
i = i + 2;これは省略して書くことができます。
// i を 2 増やす
i += 2;この省略記法は、他の四則演算に対しても用意されています。
| 演算 | 普通の記法 | 省略記法 |
|---|---|---|
| 足し算 | i = i + 2 | i += 2 |
| 引き算 | i = i - 2 | i -= 2 |
| 掛け算 | i = i * 2 | i *= 2 |
| 割り算 | i = i / 2 | i /= 2 |
for文の更新処理には再代入が使われることが多いので、この省略記法を使うとより省エネに書き進められます。例えば:
for (int i = 0; i < 100; i = i + 10) {
…
}これは以下のように省略できますね。
for (int i = 0; i < 100; i += 10) {
…
}1足す/引くに関しては、さらに特殊な記法が用意されています。
| 演算 | 普通の記法 | 省略記法 |
|---|---|---|
1 足す | i = i + 1 | i++ |
1 引く | i = i - 1 | i-- |
for文に適用するとこんな感じ。
for (int i = 0; i < 10; i = i + 1) {
…
}for (int i = 0; i < 10; i++) {
…
}広く使われているので、読めるようになっておきましょう。
for文で整列
ループ変数をうまく使うと、繰り返しで大量生産する図形を整列できます。
練習:1方向に並べる
for文を使って、横方向に整列した円を描いてみましょう。

for文のループ変数を 0 ~ 600 (キャンバス幅)まで 100 おきに変化させ、その数値をX座標として円を描けばよさそうです。
for (int x = 0; x <= 600; x += 100) {
// ループ変数 x を中心のX座標として円を描く
}(→grid_1d)
1方向のグラデーション
さて、ループ変数に入っているのはただの数値ですから、これを色に反映することもできますね。
for (int x = 0; x <= 600; x += 100) {
// ループ変数を塗り色に反映
// x: 0 で fill(0, 0, 255),
// x: 600 で fill(255, 0, 0)
// に近くなるように計算
fill(
x / 3, 0, 255 - x / 3
);
…
}
このまま図形を四角形に変更し、間隔を狭め、高さを増やしていくと…。

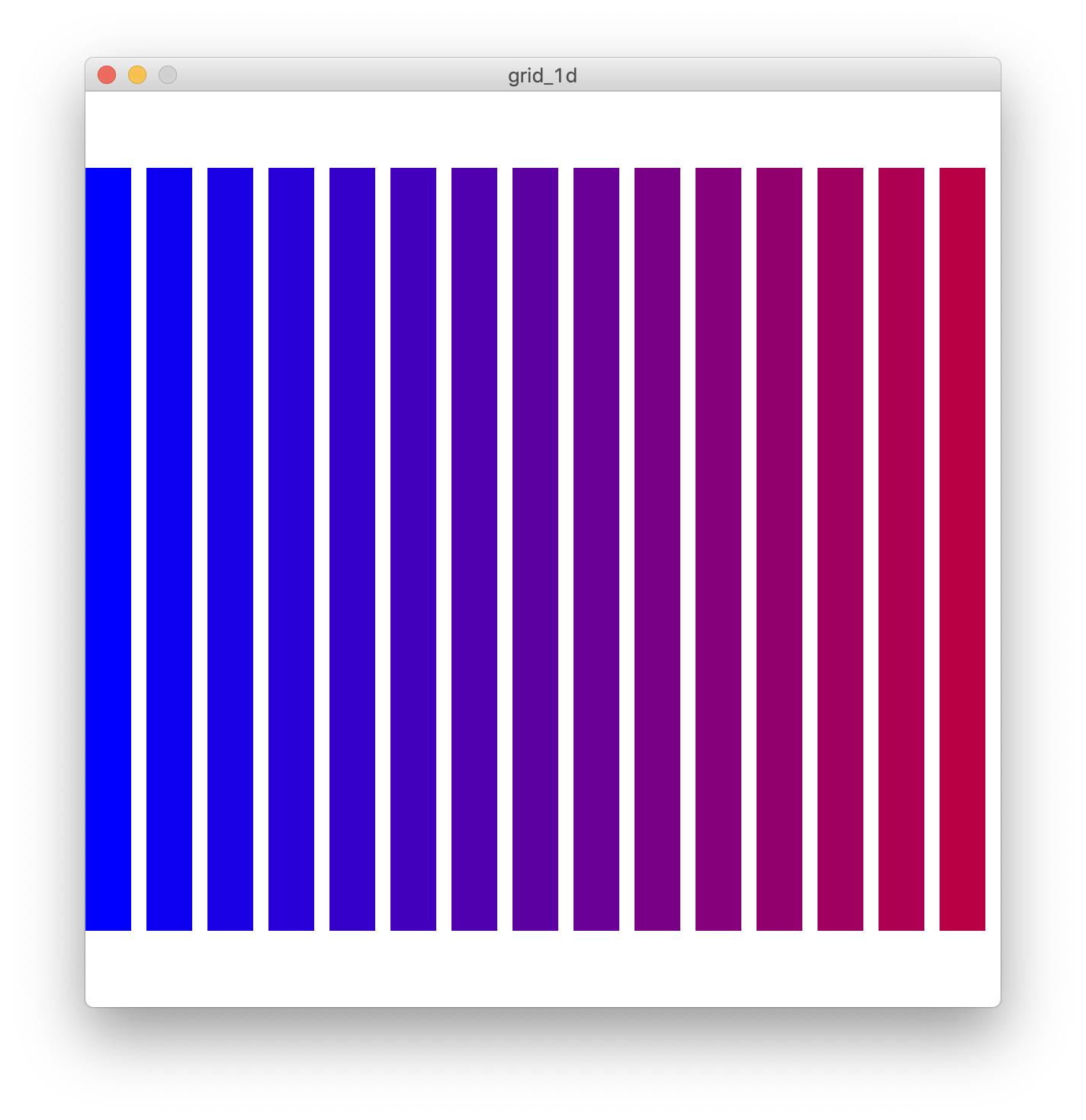

綺麗なグラデーションになりました。
(→gradient_1d)
2重のfor文
上記のスケッチは、ひとつのfor文で横(あるいは縦)1方向の整列を実現していました。
このfor文の中にさらにfor文を入れて「入れ子」にすることもできます。for文を2重にすると、縦横2方向の整列を実現できます。
2方向に並べる
2重のfor文で縦横に整列する例を見てみましょう。
(→grid_2d)
void setup() {
size(600, 600);
noStroke();
fill(0);
}
void draw() {
background(255);
// 変数 y を 0 ~ 600 (キャンバス高さ)まで、 100 ずつ増やしながら繰り返す
for (int y = 0; y <= 600; y += 100) {
// 変数 x を 0 ~ 600 まで、 100 ずつ増やしながら繰り返す
for (int x = 0; x <= 600; x += 100) {
// ループ変数を中心座標として円を描く
ellipse(x, y, 30, 30);
}
}
}
コードの分量は多くないものの、動作が複雑で理解に時間がかかりそうです…。注目すべきはこの部分。
for (int y = 0; y <= 600; y += 100) {
for (int x = 0; x <= 600; x += 100) {
// ループ変数を中心座標として円を描く
ellipse(x, y, 30, 30);
}
}挙動を紙芝居で確認してみましょう。


















練習:2方向にグラデーションさせる
2重のfor文を使えば、1方向グラデーションの応用でグラデーションを2方向に拡張できるはずです。書けるでしょうか?
(→gradient_2d)

発展
- 好きな色のグラデーションになるように狙って調整できるだろうか?
- ループ変数をセルの色ではなく、大きさや線の太さなど異なるパラメーターに反映できるだろうか?
- マウスカーソルを移動して色を変化させられるだろうか?
応用例
マウスに反応するグリッド
dist() を使うと、2点間の距離を計算することができます。
dist( 点1のX座標 , 点1のY座標 , 点2のX座標 , 点2のY座標 );for文の中で、例えば各セルの位置 ( x, y ) とカーソル位置 ( mouseX, mouseY ) との距離を計算、その数値をセルのサイズや色などに反映すると…。
void draw() {
background(255);
for (int y = 0; y <= 600; y += 20) {
for (int x = 0; x <= 600; x += 20) {
// 対象のセルとカーソル位置との距離を計算する
float d = dist(x, y, mouseX, mouseY);
// 距離をサイズに反映する(そのままでは数値が大きすぎるので小さくする)
float sz = d * 0.05;
// ループ変数を中心座標として円を描く
ellipse(x, y, sz, sz);
}
}
}
マウスカーソルに反応するインタラクティブなグリッドができますね。
(→grid_mouse)
画像と2次元グリッド
「画像」の回で、画像の色を採取する方法を学んだことを覚えているでしょうか。これと2次元グリッドを組み合わせると、画像を規則的なパターンで再構成できます。
(→grid_image)
// 画像用の変数
PImage img;
void setup() {
size(600, 600);
background(255);
noStroke();
// 画像を読み込む
img = loadImage("monalisa.jpg");
}
void draw() {
background(0);
for (int y = 0; y <= 600; y += 20) {
for (int x = 0; x <= 600; x += 20) {
// ループ変数を座標としたときの画像の色を取得
color col = img.get(x, y);
// 塗り色に設定
fill(col);
// ループ変数を中心座標として円を描く
ellipse(x, y, 10, 10);
}
}
}
色に関しては、色相や明度・彩度、赤・緑・青の度合を数値で取得できるという興味深い機能があります。
// 画像の色を採取
color col = img.get(x, y);
// 採取した色の明度をfloat型で取得
float b = brightness(col);| コード | 機能 |
|---|---|
hue() | 色相を数値で取得する |
saturation() | 彩度を数値で取得する |
brightness() | 明度を取得する |
red() | 赤を取得する |
green() | 緑を取得する |
blue() | 青を取得する |
先のスケッチと組み合わせると、いろいろとおもしろい効果を生み出せそうです。例えば、明るい(=明度が高い)ほどセルのサイズを大きくしたり(→grid_image_brightness)、色をRGBに分解してディスプレイの画素のようにしてみたり(→grid_image_rgb)…。


発展
- 乱数でセルの位置やサイズ、色に変化を加えられるだろうか?
- パラメーターを極端な数値に振ってみると、どんな結果が得られるだろうか?
- マウスカーソルに反応して位置やサイズ、色に変化を加えられないだろうか?
- 四角形や線など、円以外のセルの表現方法を何か編み出せないだろうか?
本章のまとめ
- 繰り返し回数が決まっている場合はfor文が便利
- ループ変数をうまく使うと整列できる
- for文を2重にすると縦横に整列できる