高度な配列(2次元配列)
本章のあらすじ
- 2次元配列の概要とその生成方法

2次元配列
前回は、たくさんの変数を扱うための「配列」という概念を学びました。
今回は、その配列のもう少し高度な例である「2次元配列」にも触れてみます。少々難しい題材ですが、使わなくてもそれなりにやっていけます。無理だと感じたらいったん飛ばしてしまっても大丈夫ですので、焦らずいきましょう。
2次元配列の概要
先ほどまで扱ってきた配列は1列、つまり1次元の配列でした。
Processingでは2次元のデータを扱うこともできます。縦横2方向=2次元のデータを持つ配列を「2次元配列」と呼びます。
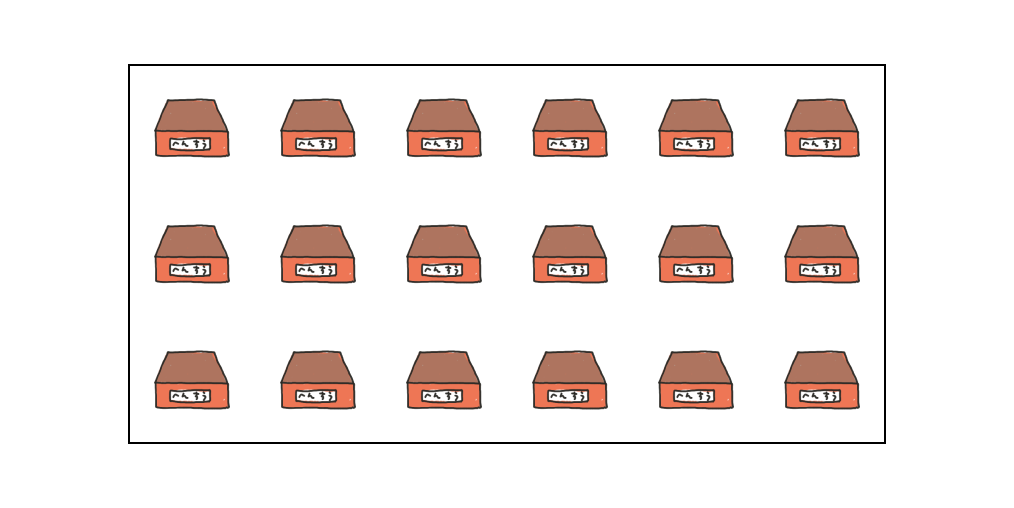
2次元配列は、変数の型にもうひとつ [] が付加されて float[][] のようになります。
// float型の2次元配列を宣言
float[][] values;1次元配列と同様、配列は宣言しただけでは空っぽです。 new で要素数を指定して領域を確保することで、はじめて各要素を使えるようになります。
// 要素数 3 × 6 の2次元配列を作成
values = new float[3][6];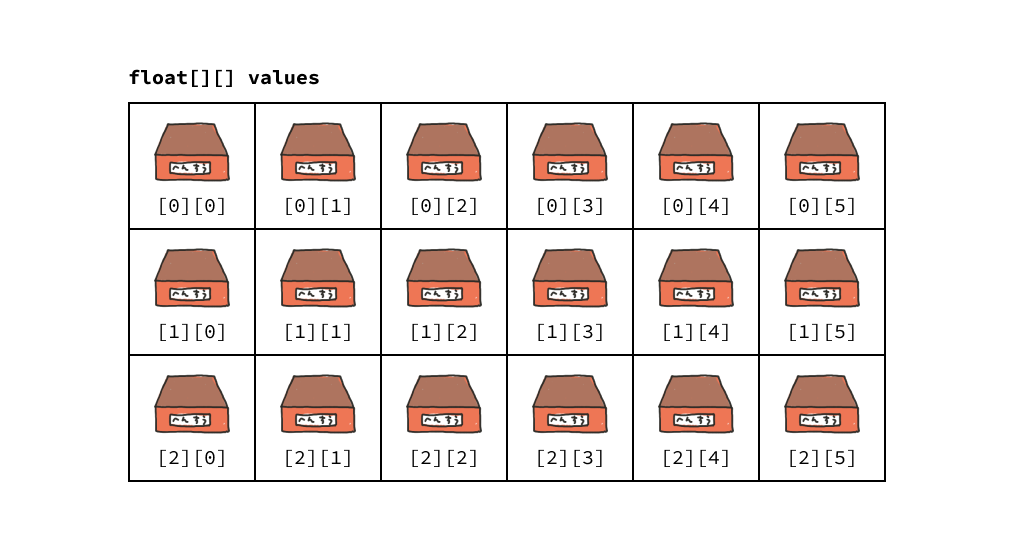
作成した配列をどう使うかは本人の自由ですが、慣習として [ 縦の要素数 ][ 横の要素数 ] という方向で利用することが多いです。本講義でもこの方向で説明していきます。
// 上から 3 番目、左から 2 番目の要素に数値を代入
values[3][2] = 1.414;練習:2次元配列を可視化してみる
まずは 31 × 31 の2次元配列を生成して各要素にランダムな数値を設定、こんな感じで可視化してみましょう。
(→grid_2d)

// 2次元配列の変数を宣言
float[][] cells;
void setup() {
size(600, 600);
noStroke();
fill(0);
// 2次元配列を生成
cells = new float[31][31];
// 2重のfor文ですべての要素に対して処理する
for (int iy = 0; iy <= 30; iy++) {
for (int ix = 0; ix <= 30; ix++) {
// 要素の値をランダムに
cells[iy][ix] = random(20);
}
}
}
void draw() {
background(255);
// 2重のfor文ですべての要素に対して処理する
for (int iy = 0; iy <= 30; iy++) {
for (int ix = 0; ix <= 30; ix++) {
// 配列の値をサイズとして利用、円を描く
float sz = cells[iy][ix];
ellipse(
ix * 20,
iy * 20,
sz, sz
);
}
}
}練習:2次元配列をランダムに変化させてみる
次に、配列の各要素をランダムに増やしてみましょう。
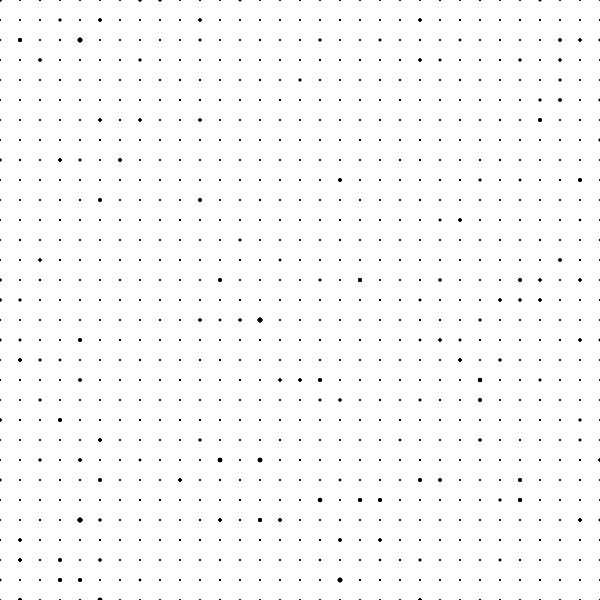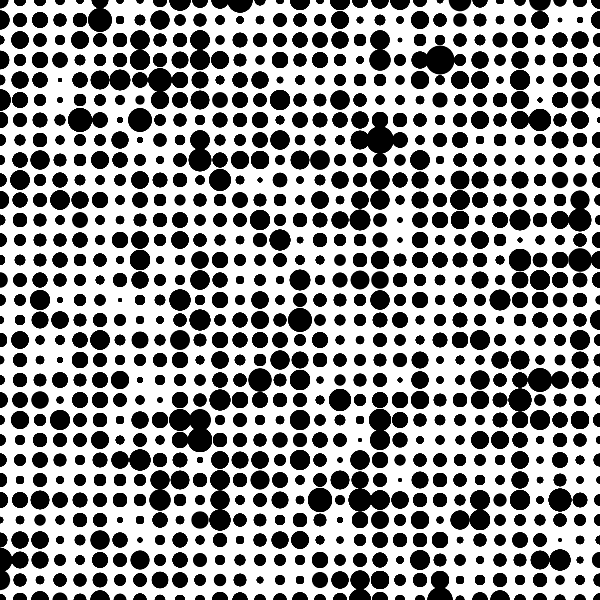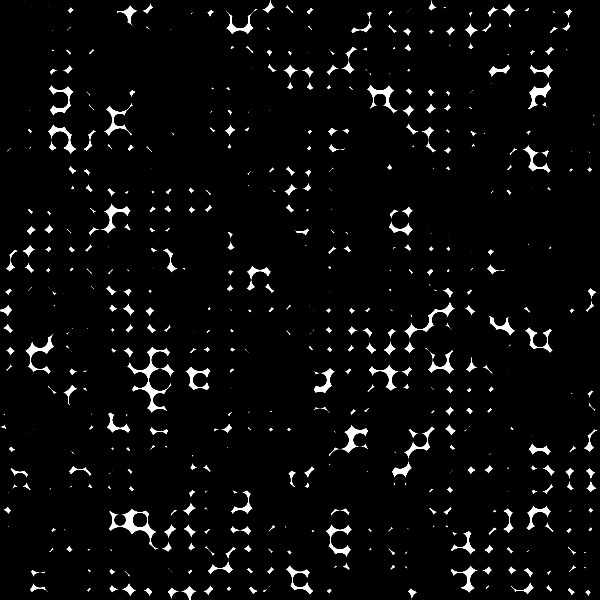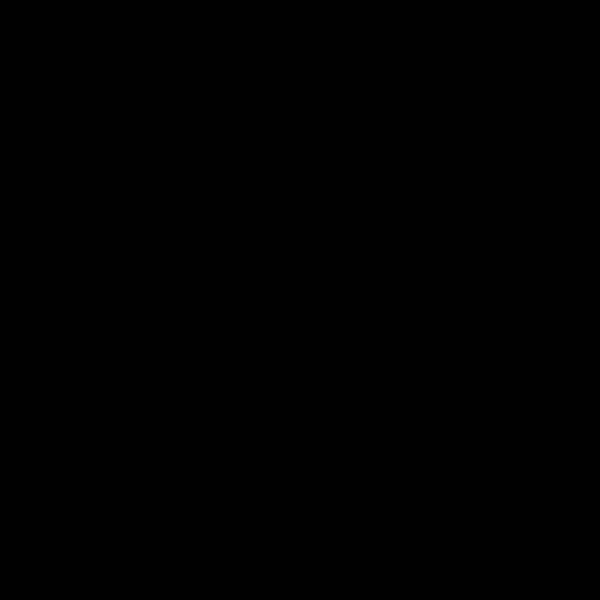
現状のランダムな初期状態では変化が見えづらいので、各要素の初期値は1にしておきましょう。
void setup() {
…
// 2重のfor文ですべての要素に対して処理する
for (int iy = 0; iy <= 30; iy++) {
for (int ix = 0; ix <= 30; ix++) {
// 要素の値を1に
cells[iy][ix] = 1;
}
}
}そして、 draw() ブロックの中にて、低確率で要素の数値を大きくしていってみます。
void draw() {
background(255);
// 2重のfor文ですべての要素に対して処理する
for (int iy = 0; iy <= 30; iy++) {
for (int ix = 0; ix <= 30; ix++) {
// 5%の確率で、ランダムに要素の数値を増やす
if (random(1) < 0.05) {
cells[iy][ix] += random(2);
}
…
}
}
}この処理によって、要素によって確率的な差はあれど、全体としてじわじわと大きくなっていく絵になります。
(→grid_2d_random)
練習:マウスと組み合わせる(インデックスの算出)
最後に、マウスと組み合わせる例を作ってみましょう。
カーソルの位置から最寄りの要素を計算して変化を加えれば、これまでにできなかったペンの表現が可能になります。例えば、最寄りの要素を少しだけ大きくする処理を書くと…。

こんな結果が得られました。
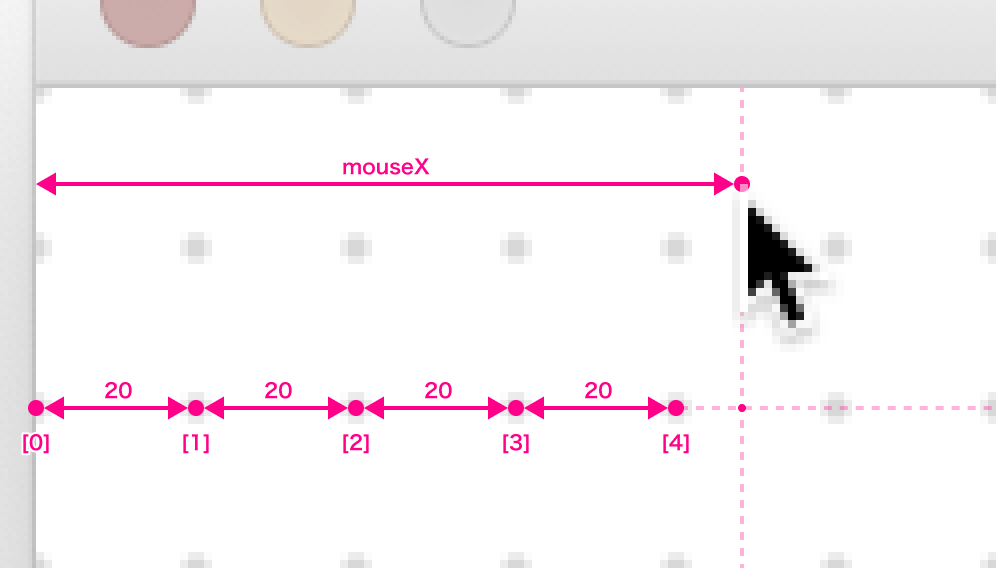
カーソル位置からインデックスを計算するのはやや難解ですが、四捨五入の round() を利用します。
void mouseDragged() {
// カーソル位置からインデックスを計算する
// 600の幅にセルが31個あるので、X座標を20で割って四捨五入すると何番目か計算できる
int ix = round(mouseX / 20.0);
// 配列の範囲を超えないように調整
if (ix < 0) {
ix = 0;
}
else if (ix >= 30) {
ix = 30;
}
// Y方向も同様
int iy = round(mouseY / 20.0);
if (iy < 0) {
iy = 0;
}
else if (iy >= 30) {
iy = 30;
}
// 該当する要素の数値を増やす
cells[iy][ix] += 2;
}カーソルの座標をセル同士の間隔で割って四捨五入すれば、何番目の要素が一番近いか=インデックスが計算できますね。
(→grid_2d_mouse)
発展
- 2次元配列の数値をセルの大きさではなく、色や形に反映できるだろうか?
- 大きくなったセルが、時間経過でだんだんと小さくなるようにできるだろうか?
mouseX / 20.0 で “.0” を書く理由:整数と小数の演算
さて、先のプログラムで一見不要とも思える .0 を書きました。
int ix = round(mouseX / 20.0);なぜ小数点をわざわざ書くのでしょうか?その理由は変数の型にあります。
以前、Processingの変数には型があるという話をしました。整数は int 、小数は float でしたね。
Processingのシステム変数 mouseX は整数 int です。 20 という数値も整数。整数同士の計算結果を、プログラムは整数と判断します。 mouseX / 20 の結果も整数。例えば mouseX が 199 だった場合、 mouseX / 20 の結果は 9.95 ではなく 9 。整数同士の計算で端数が出た場合、その結果は自動的に切り捨てられます。
一方、整数と小数の計算結果は小数と見なされます。切り捨てではなく正しく四捨五入するために、一見不要にみえる .0 を付加しているのです。
型の変換:キャスト
小数 float から整数 int に変換するには、四捨五入 round() 以外にも切り捨て・切り上げがあります。
| 変換方法 | 意味 | 例 | 結果 |
|---|---|---|---|
round() | 四捨五入 | round(5.5) | 6 |
floor() | 切り捨て | floor(5.5) | 5 |
ceil() | 切り上げ | ceil(5.1) | 6 |
逆に整数 int から小数 float に変換する手段として、数値であれば .0 を明示的に付加する方法もありますが、もうひとつ「キャスト」という機能を利用する方法もあります。
キャストは、変数の型名を書いて明示的に変換する仕組みです。変換したいものの直前に型名を丸括弧 () で囲んで付加します。
// random() によるランダムな小数を int に変換
int dice = (int)random(1, 7);ちなみに、 float から int への変換は切り捨てになります。
// random() の結果は float
// random(1, 7) は 1.0 ~ 6.9999… の範囲でランダムな数値を返す
// int にキャストして変換すると切り捨てで 1 ~ 6 になる
int dice = (int)random(1, 7);本章のまとめ
- 2次元配列は2つの軸を持つ配列
- 縦横に整列したものの状態を覚えておくために使える