THE GUILDのオフィスで定期開催しているインタラクティブコーディング勉強会、2015年の一発目のお題は「フラクタル」。（記事の公開がだいぶ遅れてしまった…）

(勉強会のまとめページはこちら)

「フラクタル」とは？

「フラクタル」。単語だけは聞いたことがある人もいるだろう。まずはWikipedia先生に聞いてみよう。

フラクタル（仏: fractale ）は、フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念。図形の部分と全体が自己相似になっているものなどをいう。 (Wikipediaより)

小難しいけど、「図形の部分と全体が自己相似」という部分が大事。Wikipediaの図をお借りして、もう少し詳しく説明してみる。

これは「マンデブロ集合」といって、フラクタル界では有名な図形。モモとヒョウタンが合体したような形をしている。この図形の白枠部分を拡大し、さらに拡大し、拡大していく。

はじめのモモヒョウタン形が、色んな部分に現れているのが見える。自分の全体の形が、一部分の形とよく似ている。全部が一部。一部が全部。これが「自己相似」。

自己相似は「シンプルなルール」で作られる

自己相似というものがわかったところで、これをどうプログラムに落とし込めばよいのか考えてみる。

一部が全部ということは、「一部を描くためのルールさえあれば、全部が描ける」ということになるはず。一部を描くためのシンプルなルールを繰り返して、全体の形を作っていく。

そのシンプルなルールをプログラム化してあげれば、フラクタルが描けそうだ。

紙で実験してみる

コードを書き始める前に、紙で簡単に実験してみよう。例えば、ここに円がある。これがフラクタルの種だ。

ここに、「円の上下左右に、少しだけ小さな円を描く」というシンプルなルールを置いてみる。この円の上下左右に、少しだけ小さな円を…

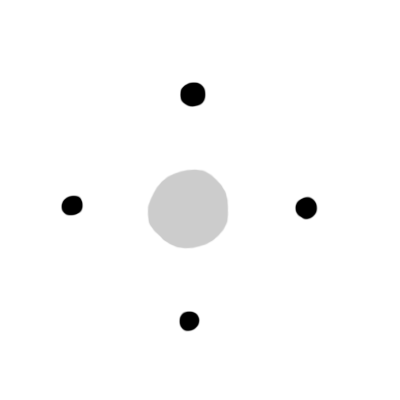
置いた。新たな円が4つ生まれた！さらにこれらの円を中心に、先ほどのルールを適用する。

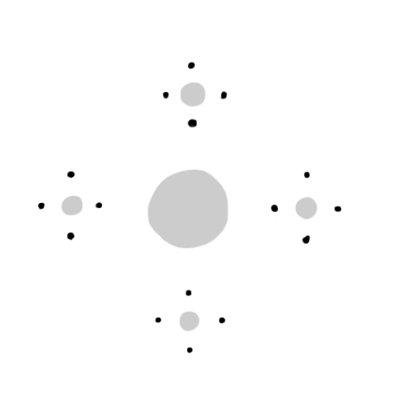
4 * 4で16個。一気に増えた。この調子でどんどん増えて、複雑な模様を描いていく。

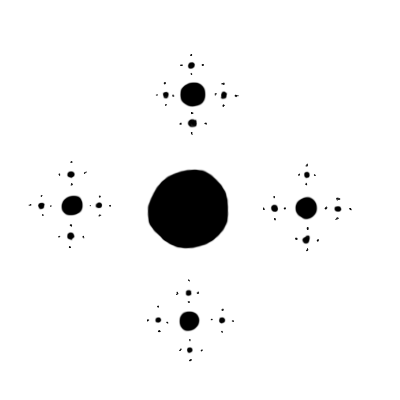
このあたりで止めておこう。すごくシンプルなルールなのに、複雑な図形が生まれていく。これがフラクタルだ。

プログラムに落とし込む

先のフラクタルを描くのにまず必要なのは、「ある点に、指定したサイズの円を描く」関数。繰り返し回数を「gen(=世代)」として、サイズをそこから計算するようにすると、こんな感じになる。

void drawCircles(int gen, float x, float y) {
  // 円を描く
  float dia = pow(SIZE_BASE, gen) * SIZE_AMOUNT;
  ellipse(x, y, dia, dia);
}

次に必要なのは、さらにそこから次の世代を描く処理。再帰処理を使って、上下左右の少し離れた位置を中心に円を描くように書き加える。

void drawCircles(int gen, float x, float y) {
  // 円を描く
  float dia = pow(SIZE_BASE, gen) * SIZE_AMOUNT;
  ellipse(x, y, dia, dia);

  // 上下左右に次の世代の円を描く
  float offset = dia * OFFSET_FACTOR;
  for (int i = 0; i < 4; i++) {
    drawCircles(
        gen + 1,
        x + cos(2 * PI * i / 4) * offset,
        y + sin(2 * PI * i / 4) * offset);
  }
}

これで第1世代の上下左右に第2世代が描かれ、さらにそれぞれの上下左右に第3世代が描かれ、…というフラクタルが完成する。が、このままだと永遠に描き続けてしまうので、ある世代で止めてあげるストッパーが必要だ。最終的にはこのようになる。

void drawCircles(int gen, float x, float y) {
  // 無限ループを防ぐため、世代が一定に達した時点で終了する
  if (gen > MAX_GENERATION) {
    return;
  }

  // 円を描く
  float dia = pow(SIZE_BASE, gen) * SIZE_AMOUNT;
  ellipse(x, y, dia, dia);

  // 上下左右に次の世代の円を描く
  float offset = dia * OFFSET_FACTOR;
  for (int i = 0; i < 4; i++) {
    drawCircles(
        gen + 1,
        x + cos(2 * PI * i / 4) * offset,
        y + sin(2 * PI * i / 4) * offset);
  }
}

作例

Dots

上で説明した例をベースに、各円に回転を加えてみた。ルールはシンプルなのに、とても複雑な動きをしているように見える。作っている本人にも制御不能な面白さが実にフラクタルらしい。

Jaggy Block

こちらも基本は同じ。パーツの形を四角形にして大きさを調整し、カタマリ感がでるように仕上げてみた。四角形から一気に崩れていくのがポイント。

Tumblrに他の作例を掲載しています。

(勉強会のまとめページはこちら)